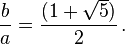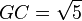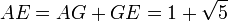PROPORCION AUREA EN UN ROSTRO

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Relación con los sólidos platónicos

El número áureo está relacionado con los sólidos platónicos, en particular con el icosaedro y el dodecaedro, cuyas dimensiones están dadas en términos del número áureo. Los 12 vértices de un icosaedro con aristas de longitud 2, pueden darse en coordenadas cartesianas por los siguientes puntos: (0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)
Los 20 vértices de un dodecaedro con aristas de longitud 2/φ=√5−1, también se pueden dar en términos similares: (±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)

Las 12 esquinas de los rectángulos coinciden con los centros de las caras de un dodecaedro.

Para un dodecaedro con aristas de longitud a, su volumen y su área total se pueden expresar también en términos del número áureo:

Si tres rectángulos áureos se solapan paralelamente en sus centros, las 12 esquinas de los rectángulos áureos coinciden exactamente con los vértices de un icosaedro, y con los centros de las caras de un dodecaedro:
El punto que los rectángulos tienen en común es el centro tanto del dodecaedro como del icosaedro.

En el pentagrama

Pentagrama que ilustra algunas de las razones áureas: los segmentos rojo y azul, azul y verde, verde y morado.

El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento, interseca a otro segmento en una razón áurea.
El pentagrama incluye diez triángulos isóceles: cinco acutángulos y cinco obtusángulos. En ambos, la razón de lado mayor y el menor es φ. Estos triángulos se conocen como los triángulos áureos.
Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea Φ. Por lo tanto el número de veces en que aparece el número áureo en el pentagrama es infinito al anidar infinitos pentagramas.

[editar] El teorema de Ptolomeo y el pentágono

Se puede calcular el número áureo usando el teorema de Ptolomeo en un pentágono regular.

Claudio Ptolomeo desarrolló un teorema conocido como el teorema de Ptolomeo, el cual permite trazar un pentágono regular mediante regla y compás. Aplicando este teorema un cuadrilátero es formado al quitar uno de los vértices del pentágono, Si las diagonales y la base mayor miden b, y los lados y la base menor miden a, resulta que b² = a² + ab lo que implica:

El rectángulo áureo de Euclides

Euclides obtiene el rectángulo áureo AEFD a partir del cuadrado ABCD. El rectángulo BEFC es asimismo áureo.

El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides en su proposición 2.11 de Los elementos obtiene su construcción.>

Con centro en G se obtiene el punto E, y por lo tanto

resultando evidente que

de donde, finalmente

Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.

Generación de un rectángulo áureo a partir de otro.

*LAS PROPIEDADES DEL NUMERO DE ORO*

http://www.youtube.com/watch?v=j9e0auhmxnc

INFORMATE ACERCA DE..........

Proporción aurea.

Relacionada también con el  número de oro es un numero  algebraico que es irracional con muchas propiedades, en este caso no es utilizado como una unidad sino como la relación o proporción entre dos segmentos de recta.  La proporción aurea se encuentra tanto en figuras geométricas y aunque no se note  en la naturaleza.

El numero áureo cumple con la expresión de que se dice que una línea recta esta divida entre el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor al menor.

El modelo de la sección aurea se caracteriza por ser la división armónica de un segmento en madia y extrema razón, que el segmento menor es al mayor y viceversa. De esa forma hay una relación en los tamaños con la misma proporcionalidad entre el todo dividido entre le mayor y el menor, es por eso que al seleccionar proporcionalmente una línea se le llama proporción aurea.

El proceso de proporción aurea también se le es conocida como espiral logarítmica pues al repetirse se obtienen una serie de rectángulos áureos encajados que convergen todos en un vértice o también conocida como espiral equiángula ya que el ángulo del corte del radio resulta ser constante con la curva.

Otro ejemplo notable de la proporción fue en el hombre que dibujo Da Vinci, ya que esta representación es perfecta por las relaciones armoniosas en las distintas partes del cuerpo lo que hace que sean proporciones áureas. Y  el cociente entre la altura del hombre que es la altura del cuadrado y la distancia del ombligo a la punta de la mano que es la circunferencia forma el número áureo.



Antecedentes históricos

En la historia de las matemáticas se establece que, alrededor del año 4700 A.C., los egipcios conocían la proporción Φ (phi) d  denominada la proporción sagrada. La proporción utilizada para la construcción de las pirámides de Gizeh es 2Φ obtenida del cociente entre la altura de cualquiera de los tres triángulos que conforman las pirámides y uno de sus lados.

Los griegos por su parte también utilizaron la proporción áurea Φ en la construcción de importantes edificios tales como el Partenón. Asimismo hicieron intervenir a Φ al esculpir obras artísticas que perduran hasta nuestros días.

La armonía entre las proporciones para hacer un trazado del hombre perfecto se plasma en el dibujo que Leonardo da Vinci hizo para ilustrar, en 1509, el libro La Divina Proporción de Luca Pacioli. La relación Φ está también presente en esta obra y se encuentra al realizar el cociente entre el lado del cuadrado y el radio de la circunferencia que tiene por centro el ombligo del hombre dibujado.

Definición Geométrica

La Proporción áurea consiste en cortar una línea en dos partes desiguales de tal manera que el segmento MAYOR sea a TODA la línea como el MENOR lo es al MAYOR.

Para hacer más claro el concepto analicemos el siguiente ejemplo:

Una línea de cualquier medida puede ser dividida o seccionada de tres maneras diferentes:

1. Si se corta  por la mitad en partes iguales se tiene una simetría simple, monótona, de relación constante y ritmo estático.

2. Si se divide por cualquier parte se produce una asimetría irracional, sin armonía, sin ritmo, ni lógica.

3. Existe una forma de seccionarla de manera que los dos segmentos resultantes guarden una relación constante y proporcional, con ritmo dinámico y recíproco, armonía equilibrada y proporción áurea.

Ésta es la Proporción Áurea geométrica cuyo exponente aritmético es conocido como

Número de Oro.

Construcción del rectángulo de oro (áureo).        

Puede construirse de la siguiente manera:

1) Constrúyase un cuadrado ABCD (por conveniencia de 2 unidades en cada lado.)

2) Divida la base AB en dos partes iguales, de lo cual se define el punto E.

3) Una E con C.

4) Trace un arco de circunferencia con radio EC y centro en E. Con esto se define el punto G en la prolongación de AB.

5) Finalmente, se obtiene el siguiente esquema:

Conclusión       

La proporción áurea tiene presencia en muchos ámbitos algunos pueden ser: en la trigonometría (donde se encuentra un triángulo áureo) y la música (en muchos ritmos existe una gran cantidad de relaciones armónicas) y representa, por lo tanto, una fuente inagotable de relaciones que existen a nuestro alrededor y de las cuales muchas veces no estamos consientes.

PROPORCIÓN AUREA

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)